Geometría analítica
La geometría analítica estudia las figuras geométricas mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas. Su desarrollo histórico comienza con la geometría cartesiana, impulsada con la aparición de la geometría diferencial de Carl Friedrich Gauss y más tarde con el desarrollo de la geometría algebraica. Actualmente la geometría analítica tiene múltiples aplicaciones más allá de las matemáticas y la ingeniería, pues forma parte ahora del trabajo de administradores para la planeación de estrategias y logística en la toma de decisiones.
Las dos cuestiones fundamentales de la geometría analítica son:
- Dado el lugar geométrico en un sistema de coordenadas, obtener su ecuación.
- Dada la ecuación en un sistema de coordenadas, determinar la gráfica o lugar geométrico de los puntos que verifican dicha ecuación.
 , donde
, donde 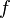 es una función u otro tipo de expresión matemática: las rectas se expresan como ecuaciones polinómicas de grado 1 (por ejemplo,
es una función u otro tipo de expresión matemática: las rectas se expresan como ecuaciones polinómicas de grado 1 (por ejemplo,  ), las circunferencias y el resto de cónicas
), las circunferencias y el resto de cónicas , la hipérbola
, la hipérbola  ), etc. como ecuaciones polinómicas de grado 2 (la circunferencia).
), etc. como ecuaciones polinómicas de grado 2 (la circunferencia).(http://es.wikipedia.org/wiki/Geometr%C3%ADa_anal%C3%ADtica)
Construcciones Funadmentales
Con la geometría analítica se puede determinar figuras geométricas planas por medio de ecuaciones e inecuaciones con dos incógnitas. Éste es un método alternativo de resolución de problemas, o cuando menos nos proporciona un nuevo punto de vista con el cual poder atacar el problema.
(http://es.wikipedia.org/wiki/Geometr%C3%ADa_anal%C3%ADtica#Construcciones_fundamentales)
Plano Cartesiano
El plano cartesiano está formado por dos rectas numéricas perpendiculares, una horizontal y otra vertical que se cortan en un punto. La recta horizontal es llamada eje de las abscisas o de las equis (x), y la vertical, eje de las ordenadas o de las yes, (y); el punto donde se cortan recibe el nombre de origen.
El plano cartesiano tiene como finalidad describir la posición de puntos, los cuales se representan por sus coordenadas o pares ordenados.
Las coordenadas se forman asociando un valor del eje de las equis a uno de las yes, respectivamente, esto indica que un punto (P) se puede ubicar en el plano cartesiano tomando como base sus coordenadas, lo cual se representa como: P(x,y)
(http://www.profesorenlinea.cl/geometria/Plano_Cartesiano.html)
Recibe su nombre al Matemático Rene Descartes
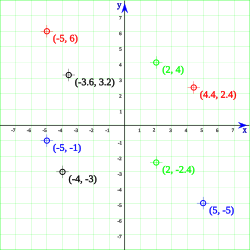
Localizacion de un punto en el plano cartesiano
En un plano traza dos rectas orientadas perpendiculares entre sí (ejes) —que por convenio se trazan de manera que una de ellas sea horizontal y la otra vertical—, y cada punto del plano queda unívocamente determinado por las distancias de dicho punto a cada uno de los ejes, siempre y cuando se dé también un criterio para determinar sobre qué semiplano determinado por cada una de las rectas hay que tomar esa distancia, criterio que viene dado por un signo. Ese par de números, las coordenadas, quedará representado por un par ordenado  , siendo
, siendo  la distancia a uno de los ejes (por convenio será la distancia al eje horizontal) e
la distancia a uno de los ejes (por convenio será la distancia al eje horizontal) e  la distancia al otro eje (al vertical).
la distancia al otro eje (al vertical).
 , siendo
, siendo  la distancia a uno de los ejes (por convenio será la distancia al eje horizontal) e
la distancia a uno de los ejes (por convenio será la distancia al eje horizontal) e  la distancia al otro eje (al vertical).
la distancia al otro eje (al vertical).
En la coordenada  , el signo positivo (que suele omitirse) significa que la distancia se toma hacia la derecha del eje horizontal (eje de las abscisas), y el signo negativo (nunca se omite) indica que la distancia se toma hacia la izquierda. Para la coordenada
, el signo positivo (que suele omitirse) significa que la distancia se toma hacia la derecha del eje horizontal (eje de las abscisas), y el signo negativo (nunca se omite) indica que la distancia se toma hacia la izquierda. Para la coordenada  , el signo positivo (también se suele omitir) indica que la distancia se toma hacia arriba del eje vertical (eje de ordenadas), tomándose hacia abajo si el signo es negativo (tampoco se omite nunca en este caso).
, el signo positivo (también se suele omitir) indica que la distancia se toma hacia arriba del eje vertical (eje de ordenadas), tomándose hacia abajo si el signo es negativo (tampoco se omite nunca en este caso).
 , el signo positivo (que suele omitirse) significa que la distancia se toma hacia la derecha del eje horizontal (eje de las abscisas), y el signo negativo (nunca se omite) indica que la distancia se toma hacia la izquierda. Para la coordenada
, el signo positivo (que suele omitirse) significa que la distancia se toma hacia la derecha del eje horizontal (eje de las abscisas), y el signo negativo (nunca se omite) indica que la distancia se toma hacia la izquierda. Para la coordenada  , el signo positivo (también se suele omitir) indica que la distancia se toma hacia arriba del eje vertical (eje de ordenadas), tomándose hacia abajo si el signo es negativo (tampoco se omite nunca en este caso).
, el signo positivo (también se suele omitir) indica que la distancia se toma hacia arriba del eje vertical (eje de ordenadas), tomándose hacia abajo si el signo es negativo (tampoco se omite nunca en este caso).
A la coordenada  se la suele denominar abscisa del punto, mientras que a la
se la suele denominar abscisa del punto, mientras que a la  ordenada del punto. se la denomina
ordenada del punto. se la denomina
 se la suele denominar abscisa del punto, mientras que a la
se la suele denominar abscisa del punto, mientras que a la  ordenada del punto. se la denomina
ordenada del punto. se la denomina
Los puntos del eje de abscisas tienen por lo tanto ordenada igual a  , así que serán de la forma
, así que serán de la forma  , mientras que los del eje de ordenadas tendrán abscisa igual a
, mientras que los del eje de ordenadas tendrán abscisa igual a  , por lo que serán de la forma
, por lo que serán de la forma  .
.
El punto donde ambos ejes se cruzan tendrá por lo tanto distancia  , así que serán de la forma
, así que serán de la forma  , mientras que los del eje de ordenadas tendrán abscisa igual a
, mientras que los del eje de ordenadas tendrán abscisa igual a  , por lo que serán de la forma
, por lo que serán de la forma  .
. a cada uno de los ejes, luego su abscisa será
a cada uno de los ejes, luego su abscisa será  y su ordenada también será
y su ordenada también será  . A este punto —el
. A este punto —el  — se le denomina origen de coordenadas.
— se le denomina origen de coordenadas.
Ecuaciones en el plano cartesiano
Una recta es el lugar geométrico de todos los puntos en el plano tales que, tomados dos cualesquiera de ellos, el cálculo de la pendiente resulta siempre igual a una constante.
La ecuación general de la recta es de la forma:
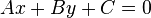
cuya pendiente es m = -A/B y cuya ordenada al origen es b = -C/B.
Una recta en el plano se representa con la Función lineal de la forma:
Como expresión general, ésta es conocida con el nombre de ecuación pendiente-ordenada al origen y podemos distinguir dos casos particulares. Si una recta no corta a uno de los ejes, será porque es paralela a él. Como los dos ejes son perpendiculares, si no corta a uno de ellos forzosamente ha de cortar al otro (siempre y cuando la función sea continua para todos los reales). Tenemos pues tres casos:
- Las rectas verticales no cortan al eje de ordenadas y son paralelas a dicho eje y se denominan rectas verticales. El punto de corte con el eje de abscisas es el punto
 . La ecuación de dichas rectas es:
. La ecuación de dichas rectas es:
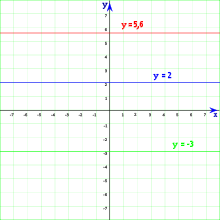
- Las rectas horizontales no cortan al eje de las abscisas y, por tanto, son paralelas a dicho eje y se denominan rectas horizontales. El punto de corte con el eje de ordenadas es el punto
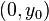 . La ecuación de dichas rectas es:
. La ecuación de dichas rectas es:
- Cualquier otro tipo de recta recibe el nombre de recta oblicua. En ellas hay un punto de corte con el eje de abscisas
 y otro punto de corte con el eje de ordenadas
y otro punto de corte con el eje de ordenadas 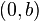 . El valor
. El valor  recibe el nombre de abscisa en el origen, mientras que el
recibe el nombre de abscisa en el origen, mientras que el  se denomina ordenada en el origen.
se denomina ordenada en el origen.
Secciones cónicas
El resultado de la intersección de la superficie de un cono, con un plano, da lugar a lo que se denominan secciones cónicas, que son: la parábola, la elipse (la circunferencia es un caso particular de elipse) y la hipérbola.
- La parábola es el lugar geométrico de todos los puntos que equidistan de un punto fijo llamado foco y de una recta fija llamada directriz.
Una parábola (figura A) cuyo eje de simetría sea paralelo al eje de abcisas se expresa mediante la ecuación:
- La elipse es el lugar geométrico de los puntos tales que la suma de sus distancias a dos puntos fijos llamados focos es siempre igual a una constante positiva, e igual a la distancia entre los vértices.
Una elipse (figura B) centrada en los ejes, con longitudes de semieje a y b viene dada por la expresión:
- Si los dos ejes son iguales y los llamamos c:
- el resultado es una circunferencia:
- La hipérbola es el lugar geométrico de los puntos tales que el valor absoluto de la diferencia (resta) de sus distancias a dos puntos fijos llamados focos es siempre igual a una constante positiva, e igual a la distancia entre los vértices.
La hipérbola (Figura C) tiene por expresión:















 puede definir cualquier función, llámese recta, circunferencia, plano, etc.
puede definir cualquier función, llámese recta, circunferencia, plano, etc.








